Дисциплина “Математический анализ” посвящена изучению функций одной и нескольких действительных переменных и их свойств.
Цели изучения дисциплины:
- Формирование математической культуры, системного мышления и основ естественнонаучного мировоззрения.
- Овладение аппаратом математического анализа, необходимым для понимания и освоения других математических, общенаучных и специальных дисциплин.
Задачи изучения дисциплины:
- Изучить логическую символику и математический язык.
- Приобрести базовые знания о функциях одной и нескольких переменных, их свойствах и различиях.
- Освоить методы исследования функций, включая особенности их поведения.
- Приобрести практические навыки вычисления пределов и производных функций одной и нескольких переменных, научиться строить их графики и находить их максимальные и минимальные значения.
Для начала изучения дисциплины достаточно знаний математики в рамках средней школы, сама же дисциплина необходима для последующего изучения остальных разделов высшей математики (интегралы, дифференциальные уравнения и т.д.).
Дисциплина разделена на два семестра и четыре модуля (см. рис. 1):
Модуль 1. Элементарные функции и пределы числовых последовательностей.
Модуль 2. Пределы и непрерывность функций одной переменной.
Модуль 3. Дифференциальное исчисление функций одной переменной.
Модуль 4. Функции нескольких переменных.
Каждый модуль заканчивается рубежным контролем, который позволяет оценить как степень освоения теоретического материала модуля, так и полученные практические навыки решения соответствующего класса математических задач. В течение каждого модуля студенты должны выполнить модульное домашнее задание, которое позволяет отработать практические навыки решения задач и подготовиться к рубежному контролю. Также после каждого семинара выдается текущее домашнее задание по пройденному на данном семинаре материалу.
Первый семестр является адаптационным с пониженной учебной нагрузкой и заканчивается зачетом. В этом семестре студенты знакомятся с порядком проведения занятий, адаптируются к системе лекция-семинар-консультация и учатся выполнять все предусмотренные контрольные мероприятия хотя бы на минимально удовлетворительном уровне в установленные сроки. Во втором семестре учебная нагрузка повышается примерно в два раза и становится равной обычной нагрузке математической дисциплины, читаемой на инженерных факультетах. По завершении второго семестра проводится письменный экзамен.
Разделение дисциплины на два семестра позволяет выстроить структуру лекций и семинаров таким образом, чтобы учесть наличие сурдоперевода, что делает процесс передачи знаний трехступенчатым – сначала преподаватель дает пояснения, сурдопереводчик его переводит, и только потом студенты делают соответствующие записи. Помимо этого, в первом адаптационном семестре много времени выделяется на правила чтения и речевое воспроизведение математических выражений. Это позволяет решить две проблемы: проблема запоминания достаточно большого объема новой информации – мы значительно легче запоминаем то, что мы можем прочитать и воспроизвести вслух – и проблема контроля степени усвоения и понимания материала – студент должен уметь не только выписывать те или иные формулы, определения и теоремы, но и объяснять их смысл.
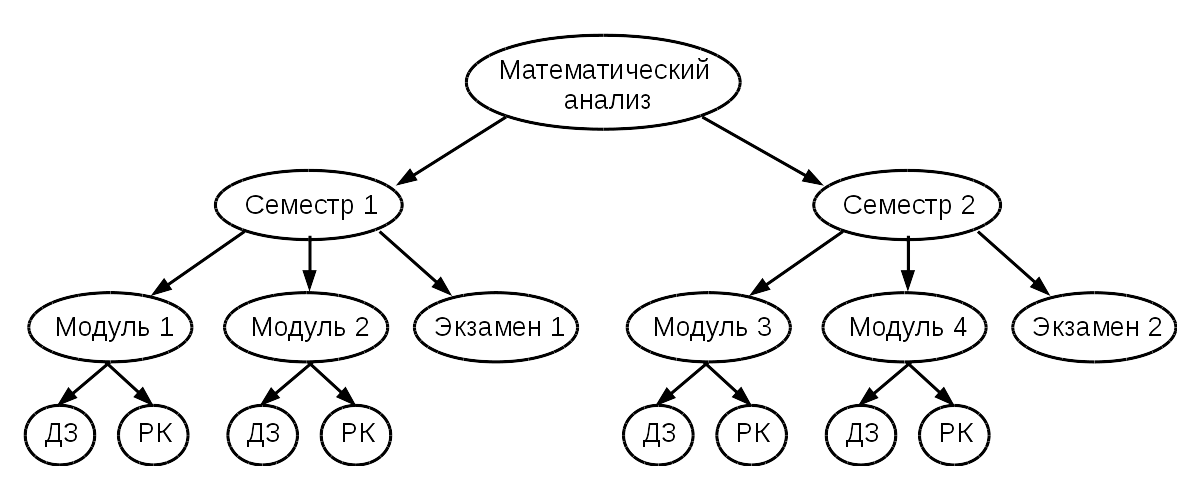
Рис. 1. Структура дисциплины
(ДЗ – модульное домашнее задание, РК – рубежный контроль)
В рамках дисциплины “Математический анализ” еженедельно проводятся следующие занятия: лекции, семинары, индивидуальные и групповые консультации. На занятиях в обязательном порядке присутствуют сурдопереводчики. В аудиториях имеются электронные доски и проекционное оборудование.
По ходу учебного процесса студентам оказывают поддержку и помогают преодолевать наиболее распространенные и часто встречающиеся проблемы несколько вспомогательных дисциплин: семантика технических текстов, когнитивные технологии и тьюторинг. Связь “Математического анализа” с этими дисциплинами показана на рис. 2. В рамках дисциплины “Семантика технических текстов” выделяется несколько занятий на правильное понимание, чтение и речевое воспроизведение наиболее часто встречающихся на лекциях математических конструкций. “Когнитивные технологии” актуализируют изучавшиеся ранее и предполагаемые известными студентам математические знания и навыки решения задач, необходимые для успешной работы на текущих семинарах по математическому анализу. В рамках тьюторинга проводятся консультации студентов по текущим учебным вопросам, осуществляется помощь с выполнением домашнего задания и проводится подготовка к рубежным контролям.
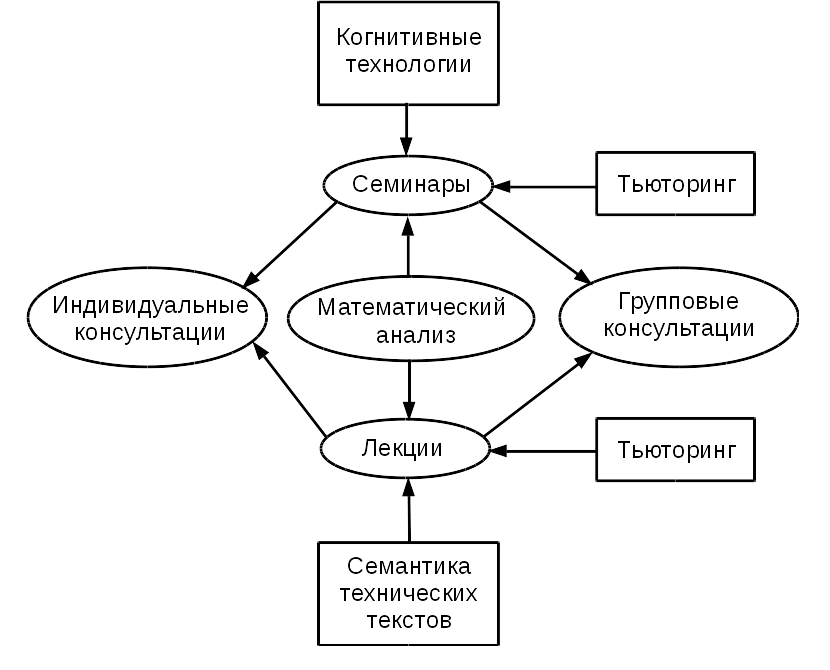
Рис. 2. Междисциплинарные связи (овалами показаны занятия, проводимые в рамках дисциплины “Математический анализ”, прямоугольниками – вспомогательные дисциплины)
В разделе “Общая информация” находятся рабочая программа дисциплины, календарные планы на оба семестра, вопросы к экзамену, примеры экзаменационных билетов, правила проведения экзаменов и список лекций с краткими аннотациями. Идущие следом разделы “Модуль 1” - “Модуль 4” содержат вопросы к рубежным контролям, примеры билетов и модульные домашние задания. Также в этих разделах приведены тексты всех лекций и соответствующих презентаций, использующихся на занятиях, что позволяет студентам либо предварительно готовиться к предстоящим занятиям, либо восстанавливать пропущенные занятия. Последний раздел “Актуализация знаний” содержит справочную информацию и материалы для работы на занятиях по вспомогательной дисциплине “Когнитивные технологии”.
Рабочая программа
Скачать:
Календарные планы
Скачать:
План работ на первый семестр - УЦ1
План работ на первый семестр - УЦ6
План работ на второй семестр - УЦ1
План работ на второй семестр - УЦ6
Экзамен
Скачать:
Теоретические вопросы к экзамену по второму семестру
Образцы билетов к экзамену по второму семестру
Аннотации лекций
Скачать:
Элементарные функции и пределы числовых последовательностей
Рубежный контроль
Скачать:
Домашнее задание
Скачать:
Лекция 1.1
Логические символы. Теорема и ее структура. Расширенное множество действительных чисел. Свойства числовых множеств и типы промежутков.
Скачать:
Лекция 1.2
Принцип вложенных отрезков. Числовая функция. Основные элементарные функции. Элементарная функция. Числовая последовательность. Конечный предел числовой последовательности.
Скачать:
Лекция 1.3
Условия сходимости числовой последовательности. Бесконечный предел числовой последовательности. Бесконечно большая последовательность. Бесконечно малая последовательность. Теоремы о конечных и бесконечных пределах. Число е и гиперболические функции.
Скачать:
Пределы и непрерывность функций одной переменной
Рубежный контроль
Скачать:
Домашнее задание
Скачать:
Лекция 2.1
Окрестность точки. Типы стремления переменной к точке. Предел функции в терминах последовательностей, окрестностей и неравенств. Арифметические свойства пределов. Односторонние пределы.
Скачать:
Лекция 2.2
Общие свойства пределов. Первый замечательный предел и его следствия. Второй замечательный предел и его следствия. Бесконечно малые функции. Бесконечно большие функции.
Скачать:
Лекция 2.3
Сравнение функций. О-большое и о-малое. Эквивалентные функции и их применение к вычислению предела. Таблица эквивалентных бесконечно малых функций.
Скачать:
Лекция 2.4
Непрерывность функций: два эквивалентных определения, необходимое и достаточное условие непрерывности. Односторонняя непрерывность слева и справа. Точки разрыва и их классификация. Свойства функций, непрерывных в точке.
Скачать:
Лекция 2.5
Свойства функций, непрерывных в точке (продолжение). Непрерывность функции на промежутке. Наклонные и вертикальные асимптоты графика функции.
Скачать:
Дифференциальное исчисление функций одной переменной
Рубежный контроль
Скачать:
Домашнее задание
Скачать:
Лекция 3.1
Производная функции, ее геометрический смысл. Односторонние производные, их связь с двусторонней производной. Дифференцируемость функции. Свойства дифференцируемых функций. Дифференциал функции, его геометрический смысл.
Скачать:
Текст 3.1 для самостоятельного изучения
Производные основных элементарных функций. Правила нахождения производных. Правила вычисления дифференциала. Приближенные вычисления значений функции с помощью дифференциала. Инвариантность формы дифференциала. Производные и дифференциалы высших порядков. Физический смысл первой и второй производных.
Скачать:
Лекция 3.2
Теоремы Ферма, Ролля, Лагранжа и Коши. Правило Лопиталя. Порядок роста функции.
Скачать:
Лекция 3.3
Формула Тейлора. Формула Маклорена. Приближенные вычисления с помощью формулы Тейлора. Монотонные функции. Экстремум функции.
Скачать:
Текст 3.2 для самостоятельного изучения
Разложение некоторых элементарных функций по формуле Маклорена. Вычисление пределов по формуле Тейлора.
Скачать:
Лекция 3.4
Условия существования экстремума. Выпуклость функции. Точки перегиба. Схема полного исследования функции.
Скачать:
Функции нескольких переменных
Рубежный контроль
Скачать:
Домашнее задание
Скачать:
Лекция 4.1
Понятие функции нескольких переменных. Предел и непрерывность. Частные производные первого порядка. Дифференцируемость.
Скачать:
Текст 4.1 для самостоятельного изучения
Типы множеств в n-мерном пространстве. Приближенные вычисления значений функций. Частные производные высших порядков.
Скачать:
Лекция 4.2
Производная сложной функции (теорема и наиболее распространенные частные случаи). Дифференциал и инвариантность его формы. Дифференциалы высших порядков. Задача о полном дифференциале.
Скачать:
Текст 4.2 для самостоятельного изучения
Неявные функции, системы неявных функций и их производные. Касательная плоскость и нормаль к поверхности. Производная по направлению и градиент.
Скачать:
Лекция 4.3
Формула Тейлора. Экстремум функции нескольких переменных. Необходимое условие. Достаточные условия по второму дифференциалу и угловым минорам. Пошаговые алгоритмы поиска точек экстремума для функций двух и трех переменных.
Скачать:
Текст 4.3 для самостоятельного изучения
Задача на условный экстремум. Необходимое и достаточное условия условного экстремума. Пошаговый алгоритм поиска условного экстремума функции двух переменных с одним ограничением. Наибольшее и наименьшее значения функции на замкнутом ограниченном множестве.
Скачать:
Лекция 4.4
Векторная функция скалярного аргумента, ее предел и производная. Векторная функция постоянной длины.
Скачать:
Текст 4.4 для самостоятельного изучения
Элементы теории кривых. Кривизная и радиус кривизны плоской кривой.
Скачать:
План работ на первый семестр:
План работ на второй семестр:
Модуль 1:
Занятие 1.1. Входное тестирование.
Занятие 1.2. Свойства и графики основных элементарных функций.
Занятие 1.3. Формулы сокращенного умножения. Исключение иррациональности из числителя или знаменателя дроби.
Занятие 1.4. Деление многочлена на многочлен. Разложение многочлена на множители методами группировки и выделения целых корней.
Модуль 2:
Занятие 2.1. Модуль действительного числа. Раскрытие знака модуля. Модульные неравенства.
Занятие 2.2-2.3. Тригонометрические формулы.
